PRODUCTOS NOTABLES

Productos notables

Sabemos que se llama producto al resultado de una multiplicación. También sabemos que los valores que se multiplican se llaman factores .

Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso.

Se les llama productos notables (también productos especiales ) precisamente porque son muy utilizados en los ejercicios.

A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable ).

Cuadrado de la suma de dos cantidades o binomio cuadrado

a 2 + 2ab + b 2 = (a + b) 2

El cuadrado de la suma de dos cantidades es igual al cuadrado de la primera cantidad, más el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.

Demostración:

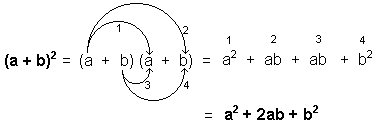
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a 2 + 2ab + b 2 debemos identificarla de inmediato y saber que podemos factorizarla como (a + b) 2

Cuadrado de la diferencia de dos cantidades

a 2 – 2ab + b 2 = (a – b) 2

El cuadrado de la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el doble de la primera cantidad multiplicada por la segunda, más el cuadrado de la segunda cantidad.

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a 2 – 2ab + b 2 debemos identificarla de inmediato y saber que podemos factorizarla como (a – b) 2

Producto de la suma por la diferencia de dos cantidades (o producto de dos binomios conjugados)

(a + b) (a – b) = a 2 – b 2

El producto de la suma por la diferencia de dos cantidades es igual al cuadrado de la primera cantidad, menos el cuadrado de la segunda

Demostración:

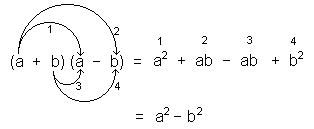
Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma (a + b) (a – b) debemos identificarla de inmediato y saber que podemos factorizarla como a 2– b 2

Otros casos de productos notable (o especiales):

Producto de dos binomios con un término común, de la forma

x 2 + (a + b)x + ab = (x + a) (x + b)

Demostración:

Veamos un ejemplo explicativo:

Tenemos la expresión algebraica

x 2 + 9 x + 14

obtenida del producto entre (x + 2) (x + 7 )

¿Cómo llegamos a la expresión?

a) El cuadrado del término común es (x)(x) = x 2

b) La suma de términos no comunes multiplicada por el término común es (2 + 7)x = 9 x

c) El producto de los términos no comunes es (2)(7) = 14

Así, tenemos:

x 2 + 9 x + 14 = (x + 2) (x + 7 )

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x 2 + (a + b)x + ab debemos identificarla de inmediato y saber que podemos factorizarla como (x + a) (x + b)

Producto de dos binomios con un término común, de la forma

x 2 + (a – b)x – ab = (x + a) (x – b)

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x 2 + (a – b)x – ab debemos identificarla de inmediato y saber que podemos factorizarla como (x + a) (x – b) .

Producto de dos binomios con un término común, de la forma

x 2 – (a + b)x + ab = (x – a) (x – b)

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma x 2 – (a + b)x + ab debemos identificarla de inmediato y saber que podemos factorizarla como (x – a) (x – b) .

Producto de dos binomios con un término común, de la forma

mnx 2 + ab + (mb + na)x = (mx + a) (nx + b)

En este caso, vemos que el término común (x) tiene distinto coeficiente en cada binomio (mx y nx) .

Demostración:

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma mnx 2 + ab + (mb + na)x debemos identificarla de inmediato y saber que podemos factorizarla como (mx + a) (nx + b) .

Cubo de una suma

a 3 + 3a 2 b + 3ab 2 + b 3 = (a + b) 3

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a 3 + 3a 2 b + 3ab 2 + b 3 debemos identificarla de inmediato y saber que podemos factorizarla como (a + b) 3 .

Cubo de una diferencia

a 3 – 3a 2 b + 3ab 2 – b 3 = (a – b) 3

Entonces, para entender de lo que hablamos, cuando nos encontramos con una expresión de la forma a 3 – 3a 2 b + 3ab 2 – b 3 debemos identificarla de inmediato y saber que podemos factorizarla como (a – b) 3 .

A modo de resumen, se entrega el siguiente cuadro con Productos notables y la expresión algebraica que lo representa:

Producto notable		Expresión algebraica	Nombre
(a + b) 2	=	a 2 + 2ab + b 2	Binomio al cuadrado
(a + b) 3	=	a 3 + 3a 2 b + 3ab 2 + b 3	Binomio al cubo
a 2 - b 2	=	(a + b) (a - b)	Diferencia de cuadrados
a 3 - b 3	=	(a - b) (a 2 + b 2 + ab)	Diferencia de cubos
a 3 + b 3	=	(a + b) (a 2 + b 2 - ab)	Suma de cubos
a 4 - b 4	=	(a + b) (a - b) (a 2 + b 2 )	Diferencia cuarta
(a + b + c) 2	=	a 2 + b 2 + c 2 + 2ab + 2ac + 2bc	Trinomio al cuadrado

CONCEPTOS BÁSICOS DEL ALGEBRA

DEFINICIÓN ÁLGEBRA

El álgebra, la mayoría de las veces da la solución mediante símbolos que representa números; esta representación numérica mediante literales o símbolos, además de operaciones que resumen las operaciones aritméticas son debidas a Galois.

 B)  Algunos conceptos básicos.

A continuación se dan algunos conceptos que nos permitirán adquirir el lenguaje para poder realizar algunas operaciones a lo largo del curso.

Una expresión algebraica es una combinación de números y letras sometidos a las operaciones de suma , resta , multiplicación , división , potenciación y radicación , que cumplen las mismas reglas que con los números.

Ejemplo:  3x² + 6xy + 3y²  

Un término es una combinación de números y símbolos (que representan números) unidos por las operaciones elementales como la suma, restas, multiplicaciones o divisiones.

Ejemplo: 9x⁵y,  -8x²/y  son términos de una expresión algebraica.

Un factor es cada uno de los componentes de un término.

Elegido un factor, un coeficiente, es lo queda del término. Si el coeficiente es un número se le llama coeficiente numérico.

Ejemplos:

Expresión algebraica	Términos	Factores	Coeficientes	Coeficientes Numéricos
a x2 + bx + b	ax2	x2	a	a,   b yc son coeficientes numéricos de los respectivos
		a	x2
	bx	x	b
		a	x
	c	c	c
4xy+1	4xy	4	xy	4 es el coeficiente numérico de 4xy
		x	4y
		y	4x
	1	1	Por ser único elemento no tiene otro coeficiente	1 es coeficiente numérico

 Se considera términos semejantes aquellos términos que se diferencian de su coeficiente numérico.  En este caso los términos se pueden reducir a un solo término.

El grado de un término es la suma de los exponentes de las variables. El grado de una constante es cero.

Expresión algebraica	Grado de la expresión
10x4z	Quinto grado
10x4z  + 1	Quinto grado
2x3y5	Octavo grado
1	Por ser una constante tiene grado cero

Una parte importante en el lenguaje algebraico es la distinción entre lo que es una identidad y lo que es una ecuación. Mientras que para una identidad formada por  dos expresiones separadas por una igualdad, donde para cada valor de su variable se cumple su igualdad, para las ecuaciones solo se cumplirá la igualdad para ciertos valores de la expresión.

Ejemplos:

Expresión	Identificación
Sen2t  + Cos2 t = 1	Identidad
X2  - 6x + 7 = 0	Ecuación
A2 + B2  =C2	Ecuación
4x /(2x-y+y)= 2	Igualdad

 Cuando sustituimos en las expresiones algebraicas en lugar de las letra o símbolos números el resultado se llama valor numérico. Una expresión algebraica puede tomar una infinidad de valores numéricos, dependiendo de los valores numéricos que les demos a las letras por esa razón a las letras que aparecen en las expresiones algebraicas se les llama variables.

Signos de agrupación de términos.

Para agrupar  términos o expresiones algebraicas se utilizan los paréntesis (), los corchetes [], o las llaves {}; generalmente las expresiones contenidas entre paréntesis se consideran como una sola cantidad. No existe una regla para dar importancia a un tipo de paréntesis con respecto a los otros, sin embargo, es usual utilizar los paréntesis () como los paréntesis para expresiones interiores, después los paréntesis [] y finalmente {}.

Ejemplo:

{3x[4zx(x+y)+w]}

¿Cuándo suprimir signos?

En ocasiones se requiere de quitar los símbolos de agrupación para lo que se tienen algunas normas:

Cuando una expresión algebraica esta agrupada mediante un paréntesis y este esta precedido de un signo positivo se puede quitar el paréntesis sin modificas los términos de la expresión. Por el contrario si  el paréntesis esta precedido de un signo menos, se puede quitar el paréntesis cambiando el signo a cada uno de los términos.

Ejemplos:

Expresión algrebraica con agrupaciones	Expresión algrebraica sin agrupaciones
+( 9x + b)	9x + b
2yz +(m - n)	2z + m – n
18x -( 2r + k –n )	18s – 2r – k + n

 Cuando una expresión cuenta con más de un paréntesis que agrupa expresiones, se comienza por los paréntesis interiores hasta llegar a los exteriores.

  

Ejemplos:

Expresión algrebraica con agrupaciones	Expresión algrebraica sin agrupaciones
(7x - (5y + 1)) + t	(7x – 5y -1)+ t =  7x – 5y + t -1
8 -((4xy)- (3xz + y))	8 - (4xy -3xz - y)) = 8 - 4xy + 3xz + y
{[(2x+1)- (xy-1)]+2xz}	{[(2x+1) - (xy-1)]+2xz}= {(2x+1) - (xy-1)+2xz}= {2x+1 – xy +1+2xz}=  2x+1 – xy + 1+ 2xz

  

CONCEPTOS ALGEBRAICOS BASICOS

OBJETIVOS:

1.- Expresar relaciones numéricas mediante símbolos numéricos y

 literales.

2.- Reconocer las expresiones algebraicas y sus elementos.

3.- Reducir y evaluar expresiones algebraicas con y sin parámetros

4.- Resolver operaciones de adición, sustracción y multiplicación de

 expresiones algebraicas.

5.- Calcular productos notables.

NOMENCLATURA ALGEBRAICA :

Variable: Es un símbolo que representa cualquier número o valor de un

conjunto dado y que puede cambiar. Normalmente se utilizan

las últimas letras del alfabeto para identificar una variable (sin que

ello sea excluyente).

Por ej: t ; x ; y ; z ; u ; v ; etc.

Constante: Es un valor fijo, que no sufre modificaciones y puede ser numérica o literal, en cuyo caso se acostumbra a utilizar las primeras letras del alfabeto para identificarlas.

Por ej: 18,  3.141516,  a, b, c, 4 etc.

Término algebraico:

Es el producto de una o más variables o una constante literal ó numérica. Están separados, entre ellos, uno de otro por un signo de suma o resta.

Por ej: 3a ; 6abx ; -acy ; 3/4 r5 ; etc.

Cuando no existe signo explícito escrito entre dos símbolos, se entiende que es multiplicación.

Monomio: Es la expresión algebraica con 1 sólo término algebraico.

Binomio : Es la expresión algebraica con 2 términos algebraicos.

Trinomio : Es la expresión algebraica con 3 términos algebraicos.

Polinomio: Es la expresión algebraica con 4 o más términos algebraicos.

Expresiones Algebraica:

Es la combinación de uno ó más términos algebraicos mediante la

operación de adición o substracción.

Por ej: 5/6ax + 2by2 − xy

 3x + 4x2 – 2/3

 ax2  + bx + c

Grado de un término algebraico:

 Es la suma de los exponentes de sus factores literales.

Por ej : -5a3c2d Grado del término = 3 + 2 + 1 = 6

 3x2  Grado del término = 2

 2/3xy2  Grado del término = 2 + 1 = 3

Orden de los términos:

En una expresión algebraica, los términos se ordenan de izquierda a derecha

3x 2 − 5x + 6xy − 3y 2

1er 2º 3er 4º término

PRODUCTOS NOTABLES:

CUADRADO DE UN BINOMIO: ( a ± b) 2 = a 2 ± 2ab + b 2

 Es igual al cuadrado del primer término, más o menos el doble producto

del primero por el segundo, más el cuadrado del segundo término.

 p. ej: ( 3x + 2 ) 2 = 9x 2 + 12x + 4

 ( x - 3y ) 2 = x 2 - 6xy + 9y 2

CUBO DE UN BINOMIO : ( a ± b) 3 = a 3 ± 3a2b + 3ab2 ± b 3

Es igual al cubo del primer término, más o menos el triple producto del

cuadrado del primero por el segundo, más el triple producto del primero por el

cuadrado del segundo, más o menos el cubo del segundo término

 p. ej: ( 2 + 3x ) 3 = 8 + 36x + 54x 2 + 27x 3

 ( 1 - 2y ) 3 = 1 - 6y + 12y 2 - 8 y 3

SUMA POR DIFERENCIA : ( a + b )( a - b ) = a 2 - b 2

 Es igual al cuadrado del primer término, menos el cuadrado del segundo

término.

 p. ej: ( x - 3 )( x + 3 ) = x 2 - 9

 ( 2y +1)(2y - 1) = 4y 2 – 1

PRODUCTO DE 2 BINOMIOS CON UN TÉRMINO EN COMÚN:

( x + a )( x + b ) = x 2 + ( a + b )x + a⋅b

 Es igual al cuadrado del término común, más la suma de los términos

diferentes por el término común, más el producto de los términos diferentes.

 p. ej: ( x + 2 )( x + 3 ) = x 2 + ( 2 + 3)x + 2⋅3 = x 2 + 5x + 6

 ( 2y +1)(2y + 3) = (2y) 2 + ( 1 + 3)⋅ 2y + 1 ⋅ 3 = 4y 2 + 4y + 3

 ( x − 3)(x + 5) = x 2 + ( − 3 + 5)⋅x + (−3)(5) = x 2 + 2x − 15